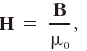A vector field, usually denoted by B, defined as follows.
The torque N experienced by a magnetic dipole with magnetic dipole moment m is
Thus by measuring N for m oriented in two orthogonal directions, the magnetic induction components are obtained as torque components divided by the magnitude of m. The fundamental relation linking electric field E and magnetic induction B to the force on a charge q with velocity v is the Lorentz force equation
Magnetic induction is sometimes called magnetic field, a term usually applied to a different field H, related to B but different from it. In free space, B and H are proportional:
where μ0, the permeability of free space, is a universal constant. B is the primitive field, whereas H is secondary, not strictly needed but convenient. Care must be exercised in deciding if, by magnetic field, B or H is meant. What is usually meant by the electric and magnetic fields (or the electromagnetic field) are E and H, although according to the Lorentz force equation E and B are the fundamental fields. Moreover, the Lorentz transformation preserves the (E, B) structure but not the (E, H) structure.