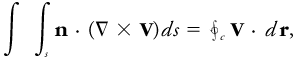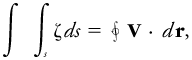Stokes's theorem
From Glossary of Meteorology
The statement that if s is a surface in three dimensions having a closed curve c as its boundary, then the circulation of a vector V around c is equal to the flux of the vorticity (curl of V) through s, under certain mathematical conditions on these fields and boundaries:
For two-dimensional flow in the x, y plane, Stokes's theorem becomes
where n is the unit vector normal to s on that side of s arbitrarily taken as the positive side. The positive direction along c is defined as the direction along which an observer, traveling on the positive side of s, would proceed while keeping the enclosed area to his left. dr is a vector line element of c.
For two-dimensional flow in the x, y plane, Stokes's theorem becomes
where ζ is the vertical component of the vorticity. This states that the circulation around a given curve per unit area enclosed by the curve is equal to the average vorticity within the area.